レーダーチャートを見せて、ゲームを魅せる 西川 俊司 [プロフィール] :1月号
前回のコラムは「見せることによって、ゲームを魅せる」というところまで説明したが、これは具体的には何を言いたいのかということから今回は話を進めたいと思う。 (1) レーダーチャートの視覚機能 まず、「経営における全体最適は部分最適に優先する」という考え方が戦略ゲームの根幹を為す中心思想であることは第1回目のコラムで述べた通りである。これを何とかゲームのなかで受講生に分かってもらいたい、しかも自分で気づいてもらいたいと思って浮かんだ方法が「レーダーチャートを見せることによって、ゲームを魅せる」ということである。と言うのは、レーダーチャートは比較される2つの主体の違いを全体として見せるだけでなく、主体を構成する主要な属性別のチャート式になっているため「どの要素を伸ばし、どれを改善すれば、全体として良くなるのか」が視角からイメージで分かるようになっているからである。 (2) レーダーチャートの面積計算による戦略性比較 さらに、戦略ゲームは4チームが8つの計画を実行して行くことによって進行する構成になっているが、この8つの計画をレーダーチャートの中心から伸びる8本の線と見做し、各チームが実行した計画の戦略性を評価し、点数付けをする仕組みをゲーム内に内蔵することによって、それらの点を結んだレーダーチャートの大きさが単なるイメージとしての大きさだけでなく、面積としての数値で表すことができるようになるのである。しかも、これは営業戦略を立てる際によく言われる話で「点より線で、線より面で攻める」と言うことをまさしく地で行くような考え方であり、理屈と実践が合致して受講生からの理解も得やすいと考える。 (3) トレイサビリティ 戦略ゲームでは、研修の振り返り時に設計の中味をむしろ公開することを推奨している。と言うのは、コンピュータゲームではしばしば設計の中に無理やり落とし穴を作ったり、実際には起こり得ない現象を入れることによって、ゲームの難易度を上げ、プレイヤーの関心を引き付けておこうとする向きがあるが、これは遊びのゲームの中では許されても、真剣な研修の中では絶対にやってはならないことである。なぜなら、知恵を絞って戦略を戦わせようとしているのに、勝敗がダイスの目によって決まるなどと言うことでは研修の教材として「支離滅裂」と言わざるを得ないからである。 これに対して、戦略ゲームはレーダーチャートに視覚機能だけでなく、ロジックとしての機能を持たせたことにより、ゲームをどの時点にでも簡単に巻き戻すことが可能になり、チャートを見ながら、「もし戦略をこのようにしていたら、結果はこうなっていたはず」ということをシミュレートすることができるのである。 「レーダーチャートの面積と全体最適の考え方」 8つの計画の評価点が下表のようなAとBの2チームのレーダーチャートを図示する。
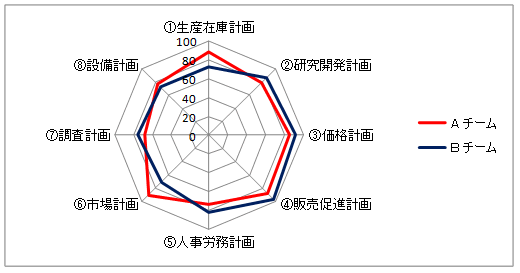 まず、AチームとBチームの評価点の合計は647で同じ点数であるが、面積の大きさはAの18,420に対し、Bは18,637と僅かながら大きいと計算される。つまり、AとBチームを線で比較すると同じ戦略性であるはずのものが、面で比較すると異なって評価されるということである。そして、その理由は線の長さで戦略性を評価する場合は、線の長さの合計だけが問題になるのであり、線の長さがバラバラであっても関係ないが、面の大きさで戦略性を評価する場合は、面を囲う2本の線の長さが揃っている方が面積は大きくなるということである。たとえば、合計が6になる整数の組み合わせを考えると、1と5、2と4、3と3になる訳だが、面積は前から順に5、8、9のように数字の近い組み合わせの方が面積は大きくなって行く。そして、これは「個々戦略が優れていても、全体が連動していなければ、経営の効率は悪くなるが、個々で優れていなくても、全体としてのバランスが取れていれば、むしろ経営効率は上がる」という戦略ゲームの思想とも合致するのである。 「面積の計算式」 レーダーチャートの面積計算であるが、いま経営に関係する計画が8つあるとして、その8本の線上につけられた点(当期の各計画に対する評価で部分最適を意味する)を結んだ8個の三角形の面積を算出して行くことから始める。 まず、三角形の面積の出し方でよく知られた計算式は、三角形の面積=底辺×高さ÷2である。しかし今回はレーダーチャートの特性からこれとは別の計算式を使うことになる。三角形の面積=2辺の長さ×sin(その2辺が挟む中心角θ)÷2という計算式である。 そして、8つの三角形の面積を合計した数値を当該チームの経営全体に対する評価とし、そのチームの経営の全体最適性を意味するものと前提しているのである。 ところで、戦略ゲームの中でロジックとして使われているレーダーチャートとエクセルで作られるレーダーチャートはじつは異なった形状になっている。と言うのは、エクセルで作られたレーダーチャートには大きな欠陥があり、そのままでは実社会の経営を評価するツールとしては使い物にならないのである。第一の問題点は中心から伸びる線の並び方の問題である。上例からエクセルでレーダーチャートを描くと、ある計画が関係する計画はその計画の両隣に座る2つの計画に限定されてしまい、経営の実態を表現できなくなってしまうのである。たとえば、価格計画は研究開発計画と販売促進計画の2つだけからしか影響されないことになってしまうという類である。第二の問題点は8つの計画の中心角がすべて同じ45°になっているということであり、これでは、その時々の経済状況や経営状況のなかで変わるはずの各計画の関係性がいつも同じということになり、戦略ゲームのプロセス重視の考え方と合致しなくなる。それより、各計画で挟まれる中心角をそれらの経営全体から見た重みと考えて、むしろ柔軟に変化できるようにした方がいろいろ違ったメリットが出て来ると思われるのである。 今回はこの辺りで留め、次回に戦略ゲームのロジック上のレーダーチャートはどのような形状になっているのか、また中心角を変えると、どのようなところに具体的なメリットが出るのか等を説明したい。 |